JS as fast as Rust!!!
Yes the title is a bit clickbaity but this article has a serious point. Don’t reach for faster programming languages before looking into how to optimise the code you already have.
TL/DR
Of course a precompiled low level language is always going to be faster than one that is not, but you can use a lot of optimisation techniques to go pretty fast without getting out the toolbox to look for something different.
Read on to find out how I made a JS solution to a problem that was just as fast as Rust and also see this solution fly in Rust.
What is faster than blazingly fast? lightning fast? ⚡
The problem
I came across this problem on youtube I’ll let ThePrimeagen explain it:
So essentially what we are doing is looking for the first unique 14 characters in a row in a given string.
Initial solution
So what does an initial solution look like?
This is an example from Mike Bostock (the dude who wrote d3):
function findStart(findString, window) {
for (let i = window, n = findString.length; i < n; ++i) {
if (new Set(findString.slice(i - window, i)).size === window) {
return i;
}
}
}
Here you can see this loops over the whole string, creates slices of that string and essentially uses a Set to quickly check if these characters are unique.
This is a great solution and only takes 3ms on my machine (or 3000000 nanoseconds this is important for later!) and if we were not trying to make something lightning fast we could stop here!
Optimising the code
Generally when I look to optimise code I look at this in three stages:
- Iterations
- How many times are we doing a given thing, can we do it on less things or cache things to make it faster?
- Computations
- What are we doing with the things we are iterating on and how can we make this faster?
- Simplifications
- Can we simplify the code, not from a reader’s perspective but for the computer to process?
Iterations
Head first jump
My initial thoughts on the problem was to loop through until we find a duplicate and then jump on to the next window of characters.
Lets take a look at a visual demo to help us see what is happening:
Here you can see us working through the input and jumping when we find a duplicate, this is fairly fast but we can go faster!
Tail first jump
This came from David’s solution which we will go into later but it is really way faster.
Again let’s take a look at a visual demo to help us see what is happening:
Here you can see we work our way back through the window of data we are looking at and it feels a lot faster.
Why is this so much faster?
Well the jump when going back through the list makes a massive difference.
Lets add in some counts to see what is going on:
Here you can see we process far less characters in my test example! whaaat?
Permutations vs Combinations
So why is this well it comes down to probabilities and in this case Combinations not Permutations.
I remember my maths teacher helping me remember this with an odd example:
Combination locks are actually permutation locks!
So in Permutations the order matters but for Combinations it does not, in our case we do not care about the order so we need Combinations and the numbers work out like this:
| Letters | Raw Chance | Simplified | One |
|---|---|---|---|
| 2 | 26/351 | 2/27 | 1/13.5 |
| 3 | 676/3276 | 13/63 | 1/4.85 |
| 4 | 8801/23751 | 677/1827 | 1/2.7 |
| 5 | 76726/142506 | 2951/5481 | 1/1.86 |
| 6 | 506051/736281 | 5561/8091 | 1/1.45 |
| 7 | 2708056/3365856 | 26039/32364 | 1/1.24 |
| 8 | 12321881/13884156 | 86167/97092 | 1/1.13 |
These are the probabilities of two letters being the same as you add more letters to the mix.
You can see as we check one more letter our chances of finding two the same get higher and higher.
This is why this code is so much faster as the probabilities are on our side, there is a high chance you find a duplicate first and skip a lot of work!
Computations
Looking at what we need to do with each letter we process we need to :
- Take the character from the string
- Check if we have seen the character before
- If we have not add it to the state
- If we have start again
- If we reach 14 we have found our solution
Character codes and Modulus
Now as we are only storing the lower characters a..z we can take the ascii/utf8 code for the characters:
'a'.charCodeAt(0) === 97;
'b'.charCodeAt(0) === 98;
// ...
'z'.charCodeAt(0) === 122;
To turn these in to numbers from 1 to 26 we can either take 96 away or more easily use the Modulus operator (which finds the remainder) to get what we want:
97 % 32 === 1;
98 % 32 === 2;
// ...
122 % 32 === 26;
So now we have a number we can use a trick called bit shifting to store all of the state for our code.
Bit shifting to store state
So this works by using a 32 bit number to store the state.
We can do this by shifting the bits over:
0b01 << 1 === 0b0010;
0b01 << 2 === 0b0100;
0b01 << 3 === 0b1000;
Note: 🤔 Here we are using the Binary Number syntax which has a 0b at the front to show that it is binary.
The << operator moves the bit to the left based on the number on the right so 0b0001 moved 2 to the left becomes 0b0100.
So we store the letters like this:
| Letters | Code | %32 | Binary (after bit shift) | Decimal |
|---|---|---|---|---|
| a | 97 | 1 | 0b000000000000000000000000010 | 2 |
| b | 98 | 2 | 0b000000000000000000000000100 | 4 |
| z | 122 | 26 | 0b100000000000000000000000000 | 67108864 |
We move the 1 over to the left to represent each letter.
This works because we are only storing 26 characters. If you ever need to store more than 64 (or maybe 128 if your language supports them) things I recommend reading up on Roaring Bitmaps I have used these in the past and they are really fast with larger bitsets. Roaring Bitmaps are one of the core technologies used by a lot of databases for faster joins and why having indexes as numbers is faster than using uuids or strings.
So why do this? well see the next operations to see how fast this can be!
Bit wise operations
So we know that computers are great with 0s and 1s, how do we go about the operations we need?
Check if we have seen the character before
So we can check if a letter has already been detected by using the & (AND) operator.
So if the state is 0b1000000000 (it has an i in it) and b comes along we can check if it is already there by:
(
0b1000000000 // 'i'
&
0b0000000100 // 'b'
) ===
0b0000000000;
This is a bitwise AND, it will return 0, if it was already there it would return 4:
(
0b1000000100 // 'i', 'b'
&
0b0000000100 // 'b'
) ===
0b0000000100; // 'b'
So we can easily check if the letter has already been seen.
If we have not add it to the state
To add the letter to the state we simply use the | (OR) operator.
We have an i in state and we want to add a b we do:
(
0b1000000000 // 'i'
|
0b0000000100 // 'b'
) ===
0b1000000100; // 'i', 'b'
Fast Mod
One thing to note here is the Fast Mod operation, now I’m pretty sure most compilers would do this anyway but it is worth knowing.
Whenever you do a modulus operation on a power of 2 e.g. 2,4,8,16,32 … you can do a faster operation by simply &ing the number minus one.
You can see this in the example below
(
0b1111010 // 122
&
0b0011111 // 31
) ===
0b0011010; // 26
So essentially 122 % 32 is the same as 122 & 31, just faster.
Simplifications
Ok this is probably the most controversial step, here we break the idioms (the usual way you would do something in a language) all together and make the code as simple as possible.
No fancy helper functions, no windowing help, we just make it as simple as possible.
We can essentially do this with two while loops:
while we still have characters to go
while we have not found a duplicate in the last 14 characters
Solutions
Ok so now armed with our knowledge let’s take a look into the solutions from the original video
Benny’s solution
pub fn benny(input: &[u8]) -> Option<usize> {
let mut filter = 0u32;
input
.iter()
.take(14 - 1)
.for_each(|c| filter ^= 1 << (c % 32));
input.windows(14).position(|w| {
let first = w[0];
let last = w[w.len() - 1];
filter ^= 1 << (last % 32);
let res = filter.count_ones () == 14 as u32;
filter ^= 1 << (first % 32);
res
})
}
This is windowing over the string in a very efficient way using a 32 bit number to store the state, and basically pushing and popping the first and last characters on and off the state whilst checking if we have reached 14.
David’s solution
pub fn david_a_perez(input: &[u8]) -> Option<usize> {
let mut idx = 0;
while let Some(slice) = input.get(idx..idx + 14) {
let mut state = 0u32;
if let Some(pos) = slice.iter().rposition(|byte| {
let bit_idx = byte % 32;
let ret = state & (1 << bit_idx) != 0;
state |= 1 << bit_idx;
ret
}) {
idx += pos + 1;
} else {
return Some(idx);
}
}
return None;
}
This is properly clever going back through each of the slices and when you find a match jumping to it, this is the Tail first jump example that I explained above.
If you carry on watching the ThePrimeagen video he does not mention the probabilities which we know is what is making it faster.
Chris’s JS solution
function findStart(findString, window) {
let state = 0;
let i = window - 1;
while (i < findString.length) {
const end = (i + 1) - window;
let w = i;
while (w >= end) {
const marker = 1 << (findString.charCodeAt(w) & 31);
if ((state & marker) === 0) {
state = state | marker;
} else {
i = w + window;
state = 0;
break;
}
if (w === end) {
return i + 1;
}
w--;
}
}
return 0;
}
This is a tail first implementation simplified to two while loops and using a number in Javascript this will be a 64 bit number but the logic still works well.
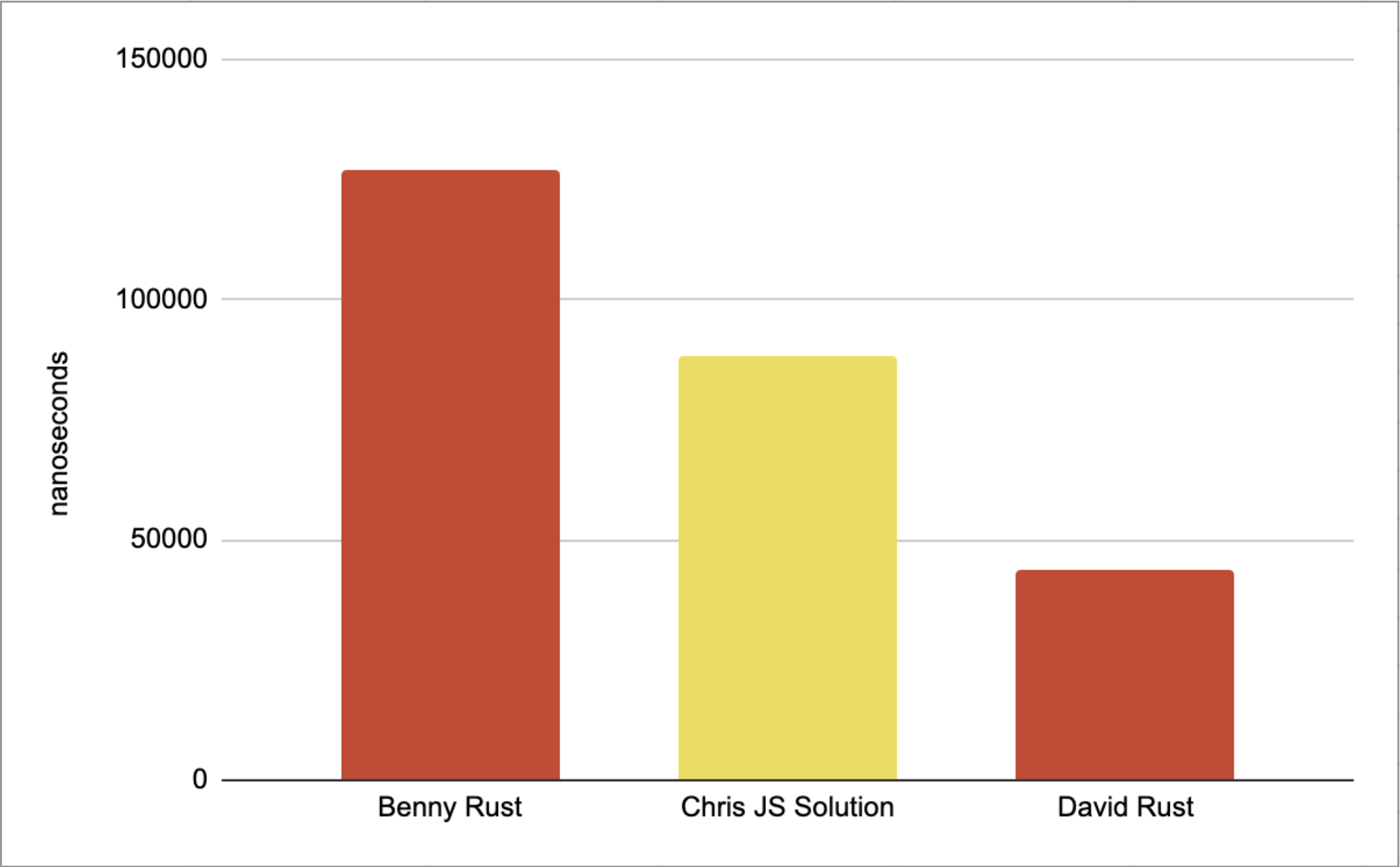
So how will this fair compared to the others!

Yep the results are in and JS holds it own against the Rust implementations!
Surely this can’t be true.

Well it is and it isn’t, let’s try the same solution in rust.
Chris’s Rust solution
pub fn chris(input: &[u8]) -> u32 {
let mut state: u32 = 0;
let input_length = input.len() as u32;
let mut i: u32 = 13;
while i < input_length {
let end = i - 13;
let mut w: u32 = i;
while w >= end {
let marker:u32 = 1 << (input[w as usize] & 31);
if (state & marker) == 0 {
state = state | marker;
} else {
i = w + 14;
state = 0;
break;
}
if w == end {
return i + 1;
}
w -= 1;
}
}
return 0;
}
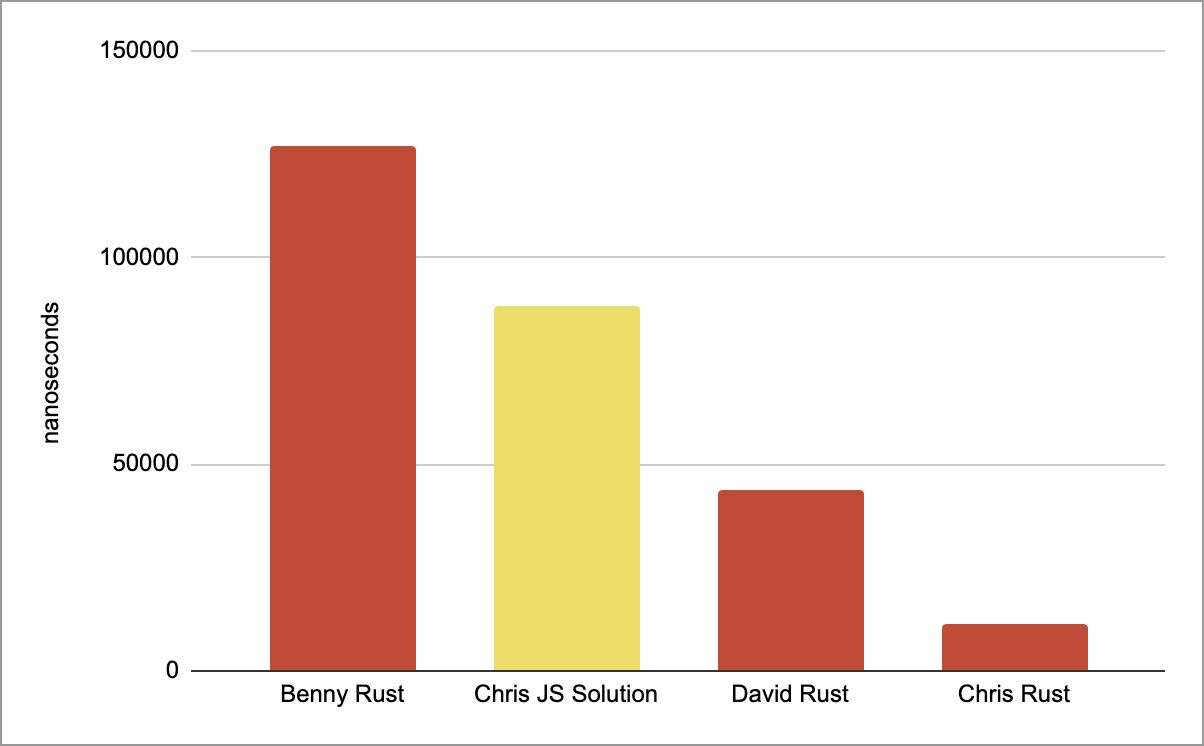
Yep this is 4x faster again! Which is pretty impressive for a simple rewrite.
Can anyone go faster? yeah I imagine so, my gut says calculating the marker each time could just be a memory lookup which would be faster but that will do for now.
Conclusion
Hopefully you found this deep dive useful and it has given you some useful insights and techniques for making your code run faster.
Would I do this all of the time? Of course not! Use the idioms of the language you are using but sometimes, just sometimes when you have a hot function (one that is called a lot by your application) it is worth knowing these techniques.
This can make a real difference to the speed of your application. It has for me a handful of times in my past.
Look after yourselves and each other.
Chris Heathwood
P.S. Do take the JS results with a sprinkling of salt, JS is a garbage collected, JIT (Just In Time) compiled, Event Loop running language so it does have other challenges when it comes to performance!